Hi again, fellow human beings. It’s me Dylan, who is also definitely a human. In this Scimatics unit, we learned about calculating surface area and volume and worked with a CAD (computer assisted design) program called Tinkercad. It is a free program and it’s easy to use (most of the time).
For this project, we had to design an object using tinkercad which was designed for either maximum surface area or maximum volume. My team was Carter, Ben Y and myself.
Reasoning and Analyzing
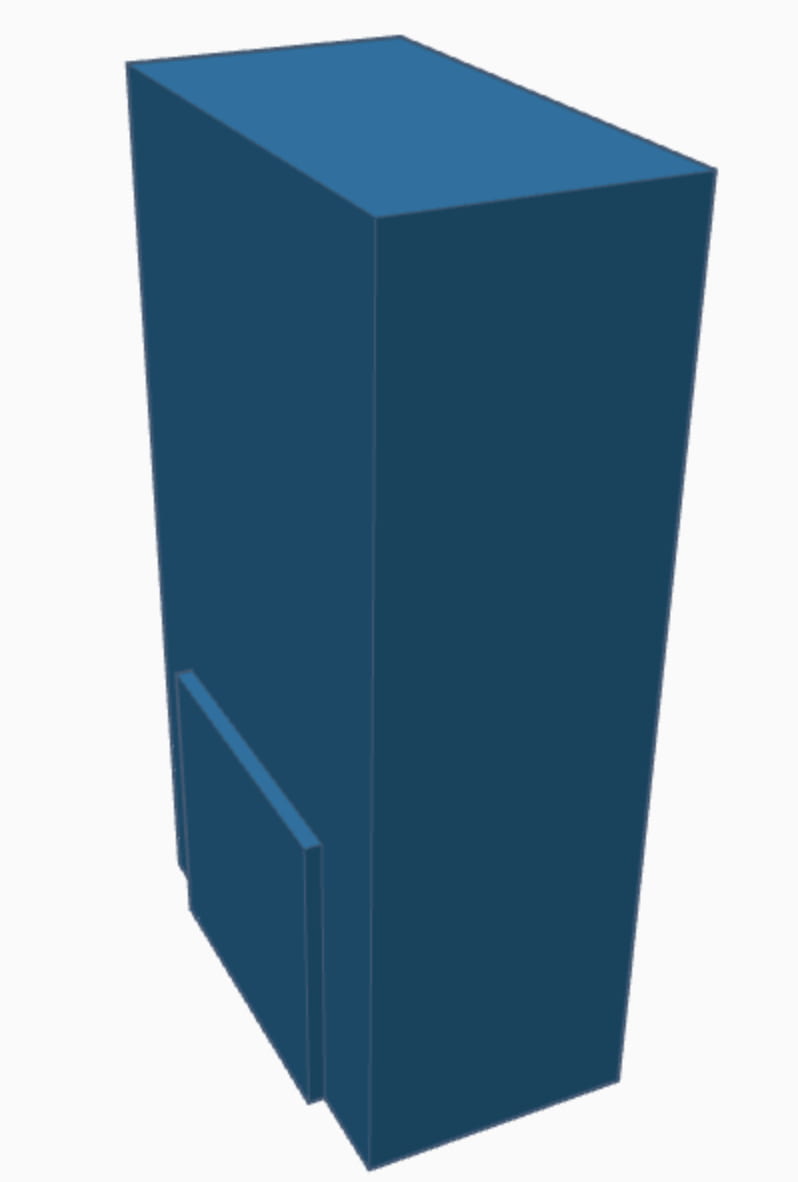
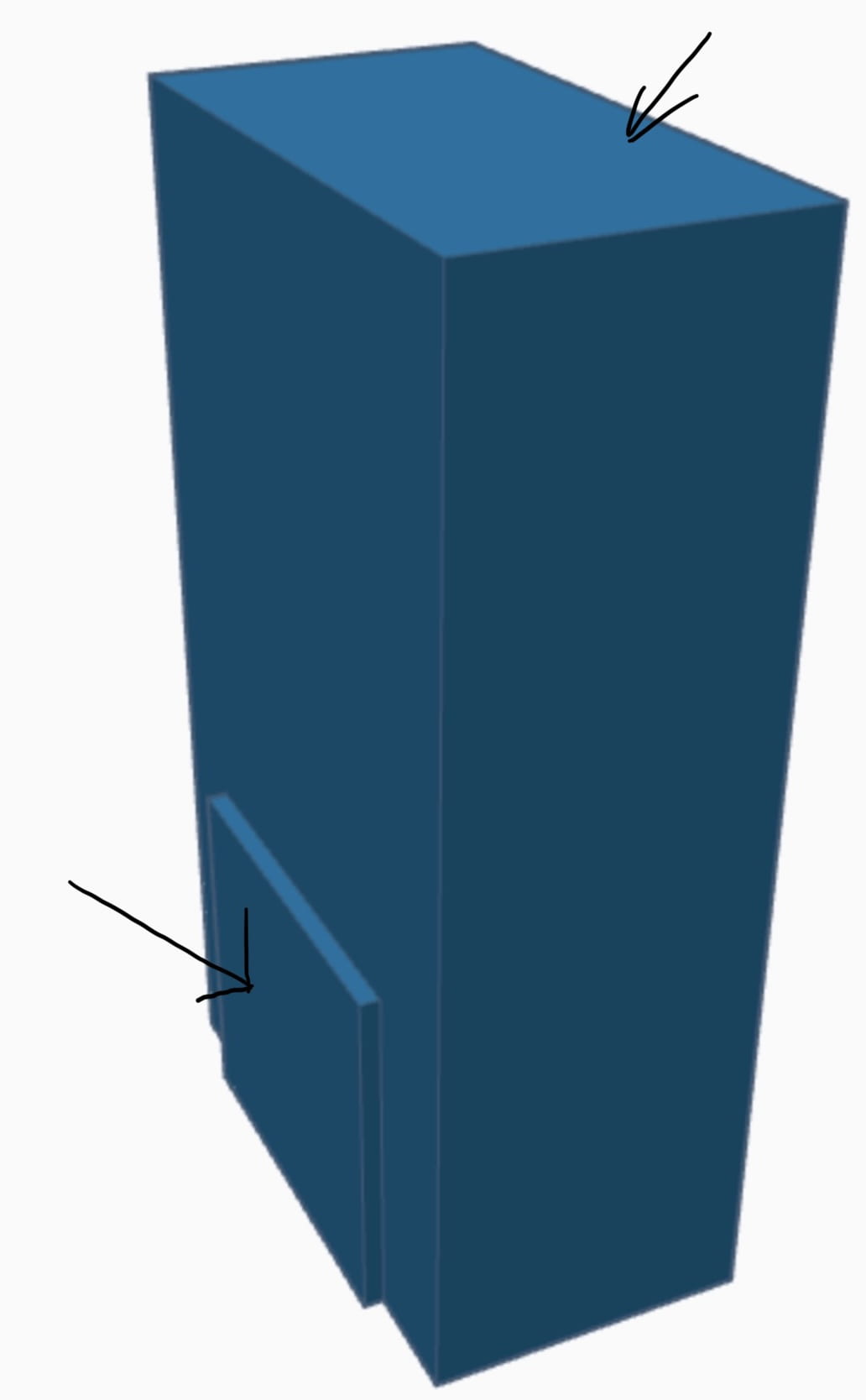
We decided that for our 3D model, we would design a garbage/recycling bin, which we would maximize for volume. Here is the full model:
Carter designed the wheels and axel and Ben did the calculations:
Ben designed the body and I did the calculations:
And I designed the lid, which carter did the calculations for:
I do have a few complaints about tinkercad, though. For one, while we were in the shared tinkercad design, every few minutes it would kick one of us out of the project and said “session lost or expired”, which was extremely annoying. Another thing is that I really wish it was a little easier to work with the shapes. I wish that there was more options to change around the shapes and throughout this project, I realized that for some shapes, tinkercad didn’t even have an option to edit them. I think we also did a fairly good job distributing the work load evenly.
Communicating and Representing
We had three different types of shapes to measure the surface and volume of: rectangular prisms, triangular prisms, and cylinders. I’ll show you the formulas we used to figure out the surface are and the volume of these shapes. I’ll use SA for surface are and V for volume.
For rectangular prisms, the formulas are:
SA= 2(l•w)+2(l•h)+2(w•h)
V= l•w•h
For triangular prisms:
SA= bh + L (S1+S2)
V= b•h
And for cylinders:
SA= 2πr²+2πrh
V= πr²h
Next, I’ll show you the calculations we used. First, I’ll show you the main part of the recycling bin, the.. well the bin.
As you can see, the bin is comprised of two rectangular prisms. One smaller and one larger. I will refer to the larger and and smaller rectangular prisms as rectangular prisms 1 and 2, respectively.
SA of rectangular prism 1
2(15.90×30)+2(15.90×52.69)+2(30×52.69) = 5790.942mm² (the measurements are in millimetres because the model needs to be small so it can be 3D printed.)
SA of rectangular prism 2
2(3xw19.16)+2(3×18.02)+2(19.16×18.02) = 917.6064mm²
Now, I was going to just add those two numbers together to the complete surface area of both rectangular prisms, but then I realized something: the back of rectangular prism 2 would need to be subtracted and so would the space it took up on rectangular prism 1, so the total SA minus the back face of the second rectangular prism and the space on the side of the other rectangular prism that it takes up x2 (690.5264²) = 6018.022mm².
V of rectangular prism 1
15.90x30x52.69 = 25133.13mm³
V of rectangular prism 2
3×19.16×18.02 = 1035.7896mm³
Total V of both rectangular prisms = 26168.9196mm³
Next is the (right) triangular prism, which was also kind of part of the main body:
The formulas to find out the volume and surface area of the right triangular prism were a little simpler than the ones used for the rectangular prisms.
Surface area
41.41+8.43+ 38.43 = 88.27mm²
Volume
30•8.43 = 252.9mm³
Now, we have the wheels
Personally, I find the formulas for finding the surface area and volume of cylinders to be kind of confusing. With this part, I will refer to the wheels as cylinders 1 and 2. The formulas are the same for both of them, since they are the same shape.
SA
2(2π • 21.06 + 2π • 20.29) = 259.809712452mm²
V
2(21.06 • 20.29) = 854.6148mm³
The last part of the recycling bin is the lid. It’s also a rectangular prism.
SA
2(30.86×20.14)+2(30.86×6)+2(20.14×6) = 40346956.32mm²
V
9.30×22.00×31.00 = 6342.6mm³
If you were confused reading that, I don’t blame you. In all honesty, I was a little confused writing it. Now, for the total SA and V:
Total SA = 19,812.157461959mm²
Total V = 33812.3159mm³
SA to V ratio = 0.58594500064:1
This means that there is 0.58594500064mm² for every 1mm³. This also means that we achieved our goal of maximizing our recycling bin for volume!
Applying and Innovating
Throughout this project, I tried my best to stay focused, and although I… um.. totally 100% didn’t zone out once or twice, I did focus almost all of the time. I also learned quite a bit about 3D modelling, which I found to be quite interesting. To be completely honest, I don’t think I’d want to work with tinkercad again as I found it to be a bit too finicky. In the future, I might want to try out other 3D modelling programs, such as Blender. I am pretty happy with what I learned in this project and I feel like a lot of the things I learned/skills I worked on will come in handy later on.
Well, that’s pretty much it! I hope you enjoyed all 831 words of this blog post and I’ll see you next time!
Bye,
Dylan.





Leave a Reply